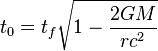Hey, folks. I thought I'd try my hoof at unlocking one of the mysteries of universe: namely, what's inside a black hole. Most ponies would state that it's impossible to know because light can't escape from a black hole and we'd never be able to see and la la la la la I can't hear you—also, I want a bazillion apples pre-cored, pre-peeled at dawn tomorrow or the diva ditches your dippy planetoid. Okay, so maybe that's just Svengallop.

Anyway, my knowledge of relativity is mostly limited to the wikipedia article. I'm not asking if what follows makes sense, because relativity usually doesn't, but if you do see an obvious error or point of contention, please point it out. Even with my limited knowledge, I did reach some interesting conclusions. There's a TLDR version at the bottom too.

Ever since the discovery of gravity waves, I've been wondering about true nature of black holes. What are they like? What's inside? Would anypony care if we tossed in Svengallop? (Apologies to anypony who likes Svengallop)

I did some research on Einstein's theory of relativity, and to my surprise, I came up with something. For simplicity, the equations I've used assume that the black hole has neither spin nor electrical charge. Adding these other properties can shrink the event horizon, but can't make it go away entirely (because then you'd have a naked singularity.) It's the properties of the event horizon itself that are important for this discussion—the size only effects the black hole's density, not the relativistic forces which determine how matter is distributed inside of it.

My hypothesis can be boiled down to this: the matter/spin/charge inside of a black hole is distributed in such a way that the escape velocity from any point inside can never exceed the speed of light.

This is a bit different from conventional wisdom which states that black holes are point-sized objects with infinite density. Before I go any further, a point I want to make clear is that gravity warps both space and time. Objects bend towards a gravitational field, and time slows down. These effects are extreme around a black hole. To get an idea of what that looks like, here's a simulation showing a merger:

This movie shows the inspiral and merger of two black holes comparable to GW150914. Shown are the horizons of the black holes as black spheres, and a representation of the warped space-time geometry as the colored surface. One hemisphere of the black hole horizons is colored, highlighting the change of rotation axis during the inspiral. The height of the colored surface illustrates curvature of space, the colors from red to green indicate how much time is slowed down near black holes, and the blue and purple colors at larger distance show gravitational waves propagating away.

This slowing down of time is known as gravitational time dilation, and has been proven by direct measurement. This is one of the results predicted by Einstein's theory of special relativity. Now now, don't let your eyes glaze over. It's actually less complicated than it sounds. To start off with, let's compare time an arbitrary distance from a gravitating object with time for an observer standing on it (assuming it's a non-charged, non-rotating sphere.) [wiki link]

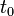is the proper time between events A and B for a slow-ticking observer within the gravitational field.

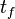is the coordinate time between events A and B for a fast-ticking observer at an arbitrarily large distance from the massive object (this assumes the fast-ticking observer is using Schwarzschild coordinates, a coordinate system where a clock at infinite distance from the massive sphere would tick at one second per second of coordinate time, while closer clocks would tick at less than that rate).

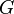is the gravitational constant.

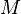is the mass of the object creating the gravitational field.

is the radial coordinate of the observer (which is analogous to the classical distance from the center of the object, but is actually a Schwarzschild coordinate).

is the speed of light.

For black holes, 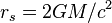is the Schwarzschild radius of 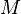, also known as the event horizon. Thus, you can simplify this further but substituting that in.

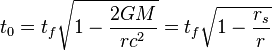
To get a sense of what that looks like, here's a graph.

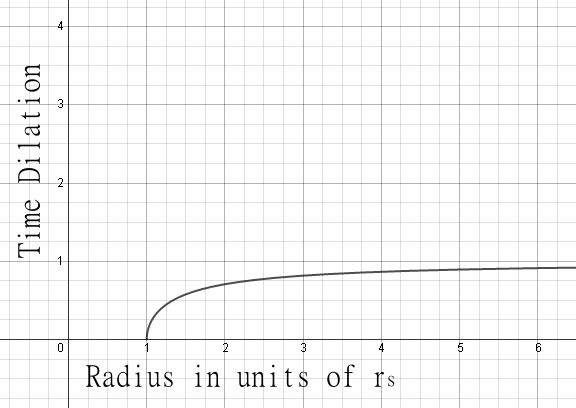
The effect of this time dilation is generally weak up until you get close to the event horizon where it rapidly plummets to zero. The value is always less than one, because that is the length of time for an object at infinite distance as measured by an observer within the gravitational field. When this value reaches zero, time effectively stops, meaning that an infinite amount of time could pass in the outside world and the observer would never witness it.

Thus, objects falling into a black hole would only be able to get as far as the event horizon before they become stuck, frozen in time and unable to fall in any further. Nothing might be able to escape a black hole, but nothing can enter one, either.

However, the event horizon can grow as the black hole eats more matter, so as it expands it will eventually swallow this frozen matter. What happens to it then? Well, let's take another look at that equation and continue plotting time dilation for distances where is inside the event horizon.

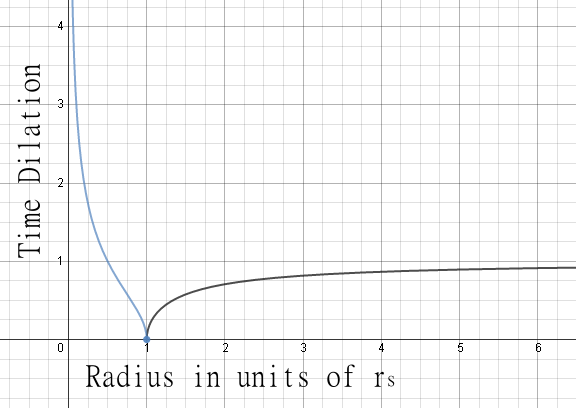
The blue line is plotted in imaginary units. Imaginary time? What does that mean?

Well, imaginary numbers can be helpful for understanding some phenomena, but in the case of black holes, this is a nonsense answer. To put it in perspective, gravitational time dilation due to mass M is equal to the relativistic time dilation of an object moving at the escape velocity from mass M. Inside the event horizon, the escape velocity is greater than the speed of light. That's silly; nothing can move faster than the speed of light. So this equation isn't helpful; something else must be going on.

To find the real answer, let's change perspectives and look at things from an object falling into a black hole. Reaching the event horizon is equivalent to traveling at the speed of light, so here's a blurb describing what that would be like. [source]

Well, if you used all the energy in the Universe for your spaceship, you could probably get up to speeds incredibly close to the speed of light. How close? The speed of light is exactly 299,792,458 meters/second. And you could get to within about 1 x 10^-30 meters/second of that value — pretty good. If you got that fast, though, what would happen? First, the entire Universe would contract to appear to only be a few billion kilometers across — less than one light year! Second, time would slow down so much, that as you would only age a few seconds, the Universe would age literally trillions of years. Galaxies would merge, stars would be born and explode in the blink of an eye. And finally, you may get to see the fate of the Universe firsthand; if the Universe has an end, you would slow down time for yourself so much that you might not only see it, you might do it in just a few seconds.

Please note that bit about witnessing the end of the universe. Seeing the entire history of the universe in an instant is what it means to be an observer who's effectively frozen in time. Now let's get back to that black hole. Due to gravitational time dilation, a massive object falling in would witness the end of the universe before crossing the event horizon, meaning, it can't.

But what about objects without mass? Light's already traveling at the speed of light, so it doesn't experience time anyway. Can it cross an event horizon? Well, no. The reason for that is similar.

Light trying to escape from a black hole experiences gravitational redshifting.

[Unedited image source]

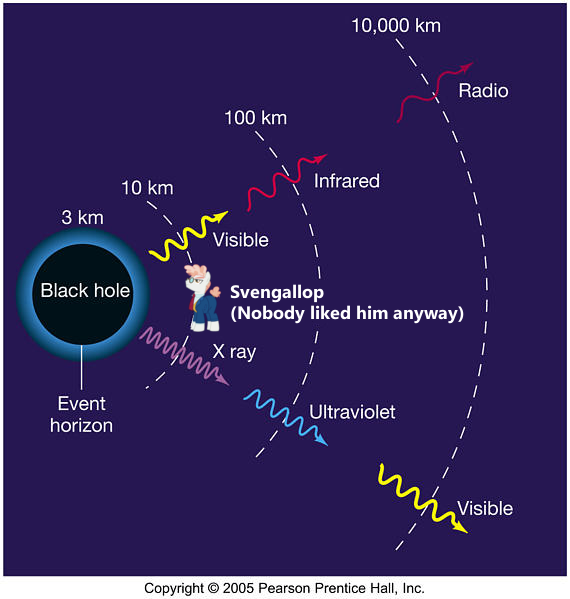
This picture shows what that's like for a black hole with a radius of 3km. At 10km out, if Svengallop gives off visible light, it will shift into the radio spectrum to an observer at 10,000 km. To see visible light at that distance, he'd have to give off x-rays. This process also happens in reverse, so at 10km out, if Svengallop had a jetpack that let him hover there, he'd be able to directly observe radio waves, while normally visible light would instead bombard him as x-rays. Aren't black holes fun?

Here's what the actual equation governing that looks like [source]:

That limit of r approaching infinity is just a fancy way of stating that the observer is at an arbitrary distance from the black hole. Re, in this case, is the radial distance from the center where the photon is emitted. rs is the Schwarzschild radius (event horizon) and ve is the initial frequency. For light, frequency and energy are essentially the same thing. If you scroll back up, you'll note that this equation looks similar to the one for gravitational time dilation. This is because frequency is measured in Hertz (cycles per second), and because this type of redshifting is caused by gravitational time dilation.

At the event horizon, the observed frequency is always zero regardless of the energy emitted. This is consistent with the concept of the event horizon being the place beyond which no light can escape. However, this process is reversible, so if you start with a fixed value of vr and solve instead for ve, you'll see that the energy of the photon becomes infinite at the event horizon.

If it's not possible for ordinary matter to achieve infinite energy, then it shouldn't be possible for a photon, either. Thus, neither ordinary matter nor light can even reach the event horizon, let alone cross it. Anything that tries to enter hits a cosmic speed limit, gets put in 'time out', and is benched until the end of the universe.

This mass increases the size of the event horizon, so new matter that falls in would get trapped at a greater distance than the old matter. If you assume that this new matter accumulates with uniform density, its gravitational pull will cancel out due to the inverse square law of gravitation inside a sphere. Thus, no point inside a black hole will have an escape velocity greater than that of the speed of light.

If that's true, then what's really inside?

Supposing that you could violate physics and journey to the center of a black hole anyway, what would you see? Well, on the surface you'd see the most recently accumulated matter, such as Svengallop because his jetpack ran out of fuel and he fell in. Layered under that, you'd see slightly older matter that got accumulated before the event horizon expanded, such as the exhaust from his jetpack. Beneath that would be older matter still. In fact, as you got closer and closer to the center, you'd witness the entire history of the black hole in reverse. In the very center would be the event which created it in the first place.

Another thing you'd witness is increasing density. The radius of the event horizon increases linearly in proportion to mass (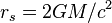), but the volume of a sphere increases proportionally to the radius cubed (Volume = (4/3) (pi)(radius)^3). Density is mass/volume, so if you do a little math, you'll note that averaged density is proportional to 1/(M^2). Halfway in, the mass of the black hole inside that radius is also half, but the volume is only an eighth, so the average density of the mass inside the halfway point would increase by a factor of four compared to the average density of the entire black hole.

In conclusion, while conventional wisdom might state that black holes are point-like objects of infinite density, this is clearly not the case. In fact, they are onion-like objects containing matter and energy frozen in timeless space. Weird, huh?

So what happens when two black holes collide? Someone gets an aneurysm, that's what.

TLDR version:

Key points:

• Nothing can travel faster than the speed of light.

• Standing upon a gravitating mass is equivalent to traveling at the escape velocity from that mass.

• At the event horizon, the escape velocity is equal to the speed of light.

This has some interesting effects:

• It's impossible for anything to cross the event horizon and enter the black hole. Doing so would increase the mass inside that radius which would cause the escape velocity to exceed the speed of light. This is forbidden because nothing can travel faster than the speed of light.

• At the event horizon, time comes to a complete stop. An observer standing on the event horizon would witness the end of the universe in an instant.

• Back holes can grow, but new mass can only be added to the surface, where it gets frozen in timeless space. The gravitational pull from this newly accumulated matter layered above the older matter cancels out such that the escape velocity speed limit is preserved even inside the expanding event horizon.

• Given that newly accreted matter always sits above older matter, if you could peel the black hole apart like an onion, you'd witness its entire history in reverse.

• Black holes are not point-sized objects of infinite density. To actually achieve that, the event horizon would also have to be point-sized, meaning that you'd have a naked singularity. The actual density increases as you get closer to the center in accordance with preserving the escape velocity speed limit.

• Einstein > Svengallop.